
Kolmogorov-Smirnov Test(KS 검정)는 데이터를 비교하여 두 데이터 세트가 동일한 분포를 따르는지 또는 한 데이터 세트가 특정 분포를 따르는지를 확인하는 비모수적 통계 검정입니다. 이 검정은 데이터가 정규 분포를 따르는지 확인하는 데 유용합니다.
Kolmogorov-Smirnov 검정(KS 검정)은 두 개의 누적 분포 함수(CDF)를 비교하여 두 데이터 세트가 동일한 분포를 따르는지 또는 주어진 데이터가 특정 분포(예: 정규 분포)를 따르는지를 평가하는 비모수적 통계 검정입니다. 이 검정은 연속형 변수에 사용되며, 특히
데이터의 분포에 대해 가정하지 않는 비모수 검정입니다.
1-표본 KS 검정 (One-sample KS test)
- 주어진 데이터가 특정 누적 분포 함수(CDF)를 따르는지 검정합니다.
- 예를 들어, 데이터가 정규 분포를 따르는지를 확인합니다.
2-표본 KS 검정 (One-sample KS test)
- 두 개의 독립적인 데이터 세트가 동일한 분포를 따르는지 검정합니다.
- 예를 들어, 두 그룹의 데이터가 동일한 분포를 따르는지를 확인합니다.

검정 절차
1-표본 KS 검정 (One-sample KS test) (주어진 데이터 vs. 특정 분포)
1. 데이터 정렬
데이터를 작은 값에서 큰 값으로 정렬합니다.
2. 누적 분포 함수(CDF) 계산
데이터의 경험적 누적 분포 함수(ECDF)와 비교하려는 분포(예: 정규 분포)의 CDF(누적 분포 함수)를 계산합니다.
3.최대 차이 계산
두 CDF 간의 최대 차이를 계산하여 KS 통계량 D를 구합니다.
식은 다음과 같습니다.
주어진 데이터 X1,X2,…,Xn의 경험적 누적 분포 함수(ECDF)를 Fn(x),
비교하려는 특정 분포의 누적 분포 함수를 F(x)라고 할 때, KS 검정 통계량 는 다음과 같이 정의됩니다.

supx는 모든 에 대한 최대 차이를 의미합니다.
4. p-value 계산 및 해석
에 대응하는 p-value를 계산하고, 이를 통해 귀무가설을 기각할지 여부를 결정합니다.
식은 다음과 같습니다. 는 오름차순으로 정렬된 데이터입니다.
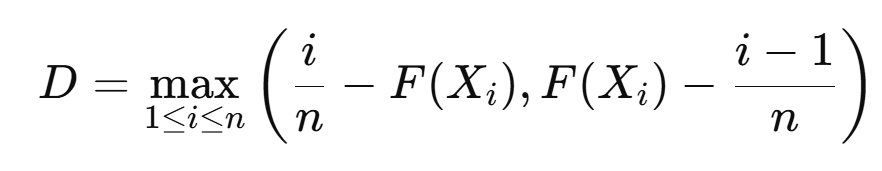
2-표본 KS 검정 (One-sample KS test) (두 개의 데이터 세트 비교)
1. 데이터 정렬
두 데이터 세트를 각각 정렬합니다.
2. 누적 분포 함수(CDF) 계산
각 데이터 세트의 ECDF(경험적 누적 분포 함수)를 계산합니다.
3.최대 차이 계산
두 ECDF(경험적 누적 분포 함수)간의 최대 차이를 계산하여 KS 통계량 를 구합니다.
식은 다음과 같습니다.
두 데이터 세트 X1,X2,…,Xn1과 Y1,Y2,…,Yn2의 경험적 누적 분포 함수를 각각 Fn1(x)와 Fn2(x)라고 할 때, KS 검정 통계량 는 다음과 같이 정의됩니다:
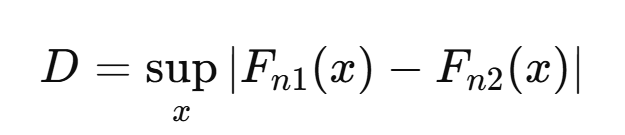
supx는 모든 에 대한 최대 차이를 의미합니다.
4. p-value 계산 및 해석
D에 대응하는 p-value를 계산하고, 이를 통해 두 데이터 세트가 동일한 분포를 따르는지 여부를 결정합니다.\
식은 다음과 같습니다.
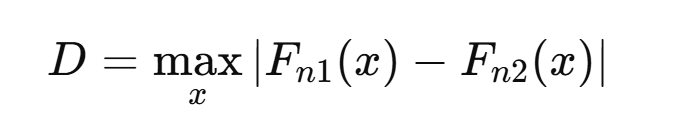
해석
p-value > 0.05(일반적으로)
귀무가설을 기각하지 않습니다.
p-value ≤ 0.05(일반적으로)
귀무가설을 기각합니다. 데이터가 해당 분포를 따르지 않는다고 결론 내립니다.
Kolmogorov-Smirnov Test(KS 검정) 의 장점
1. 비모수적 방법
특정 분포를 가정하지 않기 때문에 데이터가 정규 분포를 따르지 않아도 사용할 수 있습니다. 이는 다양한 유형의 데이터에 유연하게 적용할 수 있다는 장점이 있습니다.
2. 간단하고 직관적
최대 차이를 계산하여 분포 간의 차이를 평가하는 방식이기 때문에 계산이 비교적 간단하고 결과 해석이 직관적입니다.
3. 누적 분포 함수(CDF)를 기반으로 함
CDF(누적 분포 함수) 를 비교하여 두 분포 간의 차이를 측정하기 때문에 데이터의 전체 분포를 고려할 수 있습니다. 이는 데이터의 전반적인 분포 차이를 감지하는 데 효과적입니다
4. 작은 표본 크기에서도 사용 가능
작은 표본 크기에서도 신뢰할 수 있는 결과를 제공할 수 있습니다. 이는 데이터가 많지 않은 상황에서도 유용합니다.
5. 강력한 검정
다른 비모수적 방법들에 비해 강력한 검정력을 가지고 있어 데이터의 분포 차이를 잘 감지할 수 있습니다.
Kolmogorov-Smirnov Test(KS 검정)의 단점
1. 이산형 데이터에 부적합
KS 검정은 연속형 데이터에 적합하며, 이산형 데이터에는 적용하기 어렵습니다. 이산형 데이터에 대한 검정에서는 다른 방법을 사용하는 것이 좋습니다.
2. 큰 표본 크기에서의 민감도
큰 표본 크기에서는 매우 작은 차이도 유의미하게 나타날 수 있습니다. 이는 실제로 중요한 차이가 아닌 경우에도 귀무가설을 기각할 가능성이 있습니다.
3. 극단값(outliers)에 민감
데이터에 극단값이 포함된 경우, KS 검정 통계량이 왜곡될 수 있습니다. 이는 결과의 신뢰성을 저하시킬 수 있습니다.
4. 대응하는 p-value 계산의 복잡성
KS 검정의 p-value를 정확하게 계산하는 것은 때때로 복잡할 수 있으며, 특히 표본 크기가 클 경우 계산이 더 어려워질 수 있습니다.
코드 예시
1-표본 KS 검정 (One-sample KS test) (주어진 데이터 vs. 특정 분포)
#numpy는 배열 및 샘플 데이터 생성을 위해 사용
import numpy as np
#scipy.stats는 KS 검정을 수행하기 위해 사용
import scipy.stats as stats
#np.random.normal 함수를 사용하여 평균이 0이고 표준편차가 1인 정규 분포를 따르는 데이터 100개를 생성
data = np.random.normal(loc=0, scale=1, size=100)
#stats.kstest 함수를 사용하여 주어진 데이터가 정규 분포('norm')를 따르는지 검정
#반환값은 KS 검정 통계량 d_stat과 p-value
d_stat, p_value = stats.kstest(data, 'norm')
#검정 통계량과 p-value를 출력
print(f'KS 통계량={d_stat:.3f}, p-value={p_value:.3f}')
if p_value > 0.05:
print('데이터가 정규 분포를 따릅니다 (귀무가설 기각 안함)')
else:
print('데이터가 정규 분포를 따르지 않습니다 (귀무가설 기각)')
2-표본 KS 검정 (One-sample KS test) (두 개의 데이터 세트 비교)
#numpy는 배열 및 샘플 데이터 생성을 위해 사용
import numpy as np
#scipy.stats는 KS 검정을 수행하기 위해 사용
import scipy.stats as stats
#첫 번째 데이터 세트 data1은 평균이 0이고 표준편차가 1인 정규 분포 데이터 100개 생성
data1 = np.random.normal(loc=0, scale=1, size=100)
#두 번째 데이터 세트 data2는 평균이 0.5이고 표준편차가 1.5인 정규 분포 데이터 100개 생성
data2 = np.random.normal(loc=0.5, scale=1.5, size=100)
#stats.ks_2samp 함수를 사용하여 두 데이터 세트가 동일한 분포를 따르는지 검정
#반환값은 KS 검정 통계량 d_stat과 p-value
d_stat, p_value = stats.ks_2samp(data1, data2)
#검정 통계량과 p-value를 출력
print(f'KS 통계량={d_stat:.3f}, p-value={p_value:.3f}')
if p_value > 0.05:
print('두 데이터 세트는 동일한 분포를 따릅니다 (귀무가설 기각 안함)')
else:
print('두 데이터 세트는 동일한 분포를 따르지 않습니다 (귀무가설 기각)')'IT > 통계_용어' 카테고리의 다른 글
| [통계][용어] Shapiro-Wilk Test(샤피로-윌크 검정) (0) | 2024.07.20 |
|---|

댓글